Chama-se razão de um número racional para outro (diferente de zero), o quociente exato do primeiro pelo segundo.
Exemplo: A razão de 12 para 3 é igual a 4:
12 / 3 = 4
a / b
Lêem-se também como:
"razão de a e b " e "razão entre a e b"
A razão de um número racional para outro é sempre um número racional.
Os números racionais "a" e "b" são termos da razão; o primeiro , "a", é o antecedente e o segundo, "b", é o consequente.
Temos as seguintes condições:
1) Se o antecedente for igual ao consequente, a razão é
igual a 1.
igual a 1.
Exemplos:
2) Se o antecedente for menor que o consequente, a razão
é menor que 1.
é menor que 1.
Exemplos:
3) Se o antecedente for maior que o consequente, a razão
é maior que 1.
RAZÕES INVERSAS
Duas razões são inversas uma da outra se o seu produto é igual a 1.
Duas razões são inversas uma da outra se o seu produto é igual a 1.
O processo mais fácil de escrever a razão inversa de uma dada razão ( ≠ 0 ) é trocar entre si o antecedente com o consequente.
De maneira geral temos: dados "a" e "b", diferentes de zero, "a razão inversa de a/b é b/a; diz se que então que a/b é a razão direta.
De maneira geral temos: dados "a" e "b", diferentes de zero, "a razão inversa de a/b é b/a; diz se que então que a/b é a razão direta.
RAZÕES IGUAIS
Duas razões são ditas iguais quando as frações que as representam são equivalentes.
De maneira geral temos: dados "a" e "b (diferente de zero)", "a razão equivalente de a/b é k*a/k*b, onde "k" é o fator multiplicativo.
De maneira geral temos: dados "a" e "b (diferente de zero)", "a razão equivalente de a/b é k*a/k*b, onde "k" é o fator multiplicativo.
PROPRIEDADES
1.) Multiplicando-se ou dividindo-se os dois termos de uma razão por um mesmo número (≠ 0 ), obtém-se uma razão igual à razão dada.
2.) Para a igualdade de razões valem, como para a igualdade de números racionais, as propriedades:
- Reflexiva: a / b = a / b
- Simétrica: Se a / b = c / d, então a / d = a / b
- Transitiva: Se a / b = c / d e c / d = m / n, então, a / b = m / n
PROPORÇÕES:
Os quatro números que formam a proporção chama-se termos da proporção.
O primeiro e o quarto termos chamam-se extremos; o segundo e o terceiro termos chamam-se meios.
extremos
┌────────┐
a : b = m : n
└───┘
meios
Proporção é uma igualdade de duas razões.
PROPORÇÕES CONTÍNUAS
São proporções que têm os meios iguais.
a : b = c : d → a . d = b . c, (a, b, c, d ≠ 0)
PROPRIEDADE RECÍPROCA
Se quatro números diferentes de zero, na ordem em que estão escritos, são tais que o produto do primeiro pelo quarto é igual ao produto do segundo pelo terceiro, então os quatro números, nessa ordem, formam um proporção.
a . d = b . c → a : b = c : d, (a, b, c, d ≠ 0)
As duas implicações, a da propriedade fundamental e a da sua recíproca, podem ser reunidas numa só relação, obtendo-se assim a equivalência:
a : b = c : d ↔ a . d = b . c, (a, b, c, d ≠ 0)
PROPRIEDADE DA ADIÇÃO
Em toda proporção, a soma dos dois primeiros termos está para o primeiro (segundo) assim como a soma dos dois últimos está para o terceiro (quarto).
PROPRIEDADE DA SUBTRAÇÃO
Em toda proporção em que, para cada razão, o antecedente é maior que o consequente, a diferença entre o primeiro e o segundo termo está para o primeiro (segundo) assim como a diferença entre o terceiro e o quarto está para o terceiro (quarto).
PROPRIEDADE DA ADIÇÃO DOS ANTECEDENTES E DOS CONSEQUENTES
Em toda proporção, a soma dos antecedentes está para a soma dos consequentes assim como cada antecedente está para o seu consequente.
PROPRIEDADE DA MULTIPLICAÇÃO
Multiplicando-se membro a membro duas ou mais proporções, obtém-se ainda uma proporção.
PROPRIEDADE DA POTENCIAÇÃO
Se quatro números estão em proporção, então estão também em proporção, na mesma ordem, os seus quadrados, os seus cubos, ...



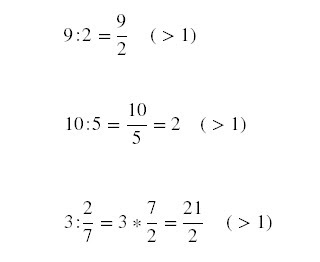






Nenhum comentário:
Postar um comentário