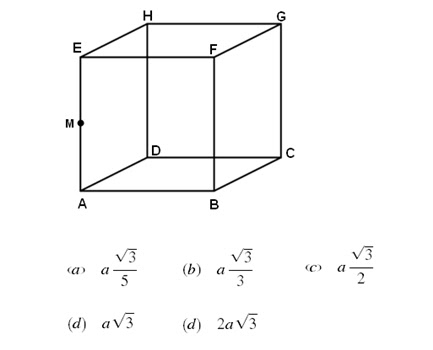
EX-01 (FUVEST - 2007)
Solução:
No triângulo retângulo da figura abaixo, aplicando Pitágoras, temos:
Resposta: a alternativa correta é (c).
EX-02 (UFSCAR - 2008)
A figura indica um
paralelepípedo retângulo de dimensões √2 x √2 x √7, sendo A, B, C e D quatro de
seus vértices.
A distância de B ao plano
que contém A, D e C é igual a:
Solução:
Como os triângulos ABC,
BCD e ACM são retângulos, por Pitágoras temos:
Portanto, o volume do
tetraedro ABCD é:
Considerando d a distância
de B até o plano ACD; e considerando o ∆ACD como base e d como a
altura do tetraedro, o volume é o mesmo. (Cálculo do volume do mesmo tetraedro
considerando parâmetros diferentes).
Portanto,
Comparando as duas
expressões do volume do tetraedro ABCD, temos:
Resposta: Alternativa correta é: b
EX-03
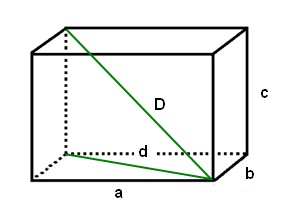
Na figura abaixo calcule
os valores de d e D em função de a, b e c.
Solução:
Na figura podemos observar as seguintes situações:
1) O segmento D é
a diagonal do paralelepípedo cujos lados são a, b e c.
2) O segmento d é
a diagonal do retângulo (=base do paralelepípedo) cujos lados são a e b.
3) Podemos observar dois triângulos retângulos (pintados de
azul e lilás) conforme a figura a seguir:
Dessa figura observa-se que o segmento d (diagonal da base
do paralelepípedo) é comum a um dos catetos do triângulo azul.
Assim podemos escrever as seguintes expressões com aplicação
de teorema de Pitágoras:
Calculando o valor da diagonal d:
De (I), temos:
Calculando o valor da
diagonal D:
(I) em (II), temos:
EX-04
Calcule a altura H do tetraedro regular de aresta a.
Solução:
Aplicando Pitágoras no
triângulo retângulo ∆ABM1, temos:
EX-05
Calcule a altura H do pentaedro regular de aresta a.
A altura H é o cateto do triângulo BEO, retângulo em O.
1) Calcular o valor do segmento OB (cateto do ∆BEO):
O triângulo ∆ABD
é retângulo em A, portanto, temos:
2) Calcular o valor da
altura H:
O triângulo ∆BEO é retângulo em O, portanto, temos:
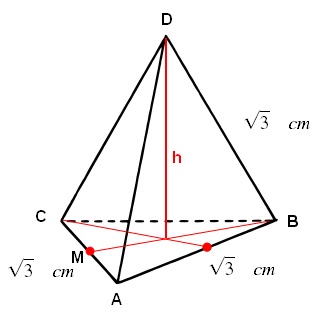
EX-06
Uma empresa produz dados
com 4 faces em forma de tetraedro regular. Os dados são feitos de acrílico e
sua aresta mede √3 cm. O volume de acrílico utilizado para
fabricar 5000 dados é:
a) 1200√6 cm3
b) 1250√6 cm3
c) 1300√6 cm3
d) 1350√6 cm3
e) 1400√6 cm3
Solução:
Sabendo-se que:
Então,
O volume do tetraedro é um
terço do produto da área da base pela altura h.
O volume de acrílico
necessário para fabricar 5000 dados é:
Resposta: alternativa b
EX-07 (FUVEST/ENEM)
Os vértices de um
tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse
tetraedro é:
a) 2√3
b) 4
c) 3√2
d) 3√3
e) 6
Solução:
As arestas do tetraedro
ACHF são as diagonais da face do cubo, então:
A área de uma face desse
tetraedro é igual à do triângulo equilátero de lado 2√2. Então.
Logo, temos:
Resposta: alternativa a








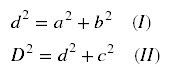















Nenhum comentário:
Postar um comentário